Windows 11 の設定
ASUS TUF
アマゾンタイムセールで 156K が 135K くらいに。
- キーボード設定
PowerToys の Keyboard Manager では期待通りに変更できず。正確には、CAPS LOCK (VS 240 1と認識される) を Ctrl (Left) へマップすると、一度 CAPS LOCK ボタンを押すとそのあとは Ctrl ボタンを押下した状態を維持してしまう。
そのため、Ctrl2Cap を使ったところ、うまくいった。
Edge のタブ間の移動や、Delete ボタンなどは PowerToys でショートカットの再マップにより問題なく設定することができた。シェルにおいて直近の履歴を確認するショートカットと重複するので、対象のアプリには msedge を設定しておく。なお、縦タブへは Edge の標準の設定で変更可能。
- WSL2設定
とりあえず zinit ではなく oh-my-zsh を入れて、テーマとして agnoster を入れたかったが、フォントをインストールする必要があった。PowerShell から、 WSL2 (Ubuntu) のファイルシステム (\wsl$\ubuntu) へアクセスして、install.ps を実行するも完了せず。
WSL2 側に C ドライブがマウントされている2ので、そちらへ mv してから、エクスプローラーから実行したところ、フォントのインストールに成功した。WSL のプロパティのフォントにおいて、インストールされたフォントを選択。
ただし、Ubuntu on Windows ではどうしてもインストールしたフォントを選択した設定が維持されない。開きなおすともともと設定してあったフォントに変更されてしまうため使いたくない。これは、Windows Terminal の既定のプロファイルを Ubuntu にして起動することで対処することができた。Windows 上で検索するときには、Terminal と入力するとコマンドプロンプトしか表示されないため、日本語でターミナルと入力する必要がある。これをタスクバーにピン留めした。
なお、プロパティのオプションの、Ctrl+Shift + C/V をコピー/貼り付けとして使用する、にチェックを入れることで、WSL からクリップボードへアクセスしている。
ファイルやディレクトリの探し方まとめ
完成
実践
- /usr/で実践
- リンクファイルがあると末尾に@がつくためFile not foundになったり、空白をファイル名に含む場合にうまくソートできなかったり、ファイルが無いディレクトリだとディレクトリを表示してしまったり、等を修正。
user:[~]$ for dir in $(find /usr/ -type d | grep -vxF .); do echo "$(ls -1 $dir | wc -l) $dir"; done | sort -rn | head -n 10 3295 /usr/share/app-install/desktop 2103 /usr/share/app-install/icons 1973 /usr/share/man/man3 1910 /usr/lib/x86_64-linux-gnu 1890 /usr/share/doc 1723 /usr/bin 1682 /usr/share/man/man1 1568 /usr/src/linux-headers-4.8.0-52-generic/include/config 1568 /usr/src/linux-headers-4.8.0-36-generic/include/config 1180 /usr/src/linux-headers-4.8.0-52/include/linux user:[~]$ for dir in $(find /usr/ -type d | grep -vxF .); do stat "$dir/$(ls -S --file-type $dir | egrep -v "[/@]$" | head -n1)" --format="%s %n"; done | grep -v "/$" | sort -rn | head -n 10 103581280 /usr/lib/x86_64-linux-gnu/libOxideQtCore.so.0 75839136 /usr/lib/thunderbird/libxul.so 72949536 /usr/lib/firefox/libxul.so 58131384 /usr/lib/libreoffice/program/libmergedlo.so 39688256 /usr/lib/x86_64-linux-gnu/webkit2gtk-4.0/WebKitPluginProcess2 26068668 /usr/share/tegaki/models/zinnia/handwriting-ja.model 23701384 /usr/lib/mozc/mozc_server 22427896 /usr/lib/gcc/x86_64-linux-gnu/5/cc1plus 19319840 /usr/share/fonts/opentype/noto/NotoSansCJK-Bold.ttc 18597793 /usr/share/mythes/th_en_US_v2.dat user:[~]$ for dir in $(find /usr/ -type d | grep -vxF .); do stat "$dir/$(ls -t --file-type $dir | egrep -v "[/@]$" | head -n1)" --format="%Y %n"; done | grep -v "/$" | sort -rn | head -n 10 1495553004 /usr/lib/python3.5/xml/dom/__pycache__/NodeFilter.cpython-35.pyc 1495553004 /usr/lib/python3.5/json/__pycache__/encoder.cpython-35.pyc 1495553004 /usr/lib/python3.5/email/mime/__pycache__/nonmultipart.cpython-35.pyc 1495542287 /usr/lib/python2.7/dist-packages/pygtkcompat/pygtkcompat.pyc 1495542287 /usr/lib/python2.7/dist-packages/gtweak/tweaks/tweak_group_interface.pyc 1495542287 /usr/lib/python2.7/dist-packages/gtweak/__init__.pyc 1495542287 /usr/lib/python2.7/dist-packages/gi/repository/__init__.pyc 1495542287 /usr/lib/python2.7/dist-packages/gi/overrides/GIMarshallingTests.pyc 1495542287 /usr/lib/python2.7/dist-packages/gi/_gobject/__init__.pyc 1495542287 /usr/lib/python2.7/dist-packages/gi/_error.pyc user:[~]$ du -sh /usr/ 3.4G /usr/ user:[~]$ du -s --inode /usr/ 200085 /usr/ user:[~]$ find /usr/ -type f | wc -l 116407 user:[~]$ find /usr/ -type d | wc -l 20743 user:[~]$ find /usr/ -type l | wc -l 62938 user:[~]$ find /usr/ -mmin -1440 | wc -l 18
練習
[~/Work]$ for dir in $(seq 1 100);do mkdir dir_$dir; cd dir_$dir; for file in $(seq 1 100);do touch file_$file; done; for sub in $(seq 1 10); do mkdir sub_$sub; cd sub_$sub; for file in $(seq 1 100); do touch sub_file_$file; done; cd ..; done; cd ..; done
[~/Work]$ touch dir_100/file_101 [~/Work]$ cat dir_100/file_101 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000
- ファイル数が多いディレクトリTop10
[~/Work]$ for dir in $(find . -type d | grep -vxF .); do echo "$dir $(ls -1 $dir | wc -l)"; done | sort -r -k 2 | head -n 10 ./dir_100 111 ./dir_99 110 ./dir_98 110 ./dir_97 110 ./dir_96 110 ./dir_95 110 ./dir_94 110 ./dir_93 110 ./dir_92 110 ./dir_91 110
- 修正した時間が直近のファイルTop10
[~/Work]$ for dir in $(find . -type d | grep -vxF .); do echo "$(stat $dir/$(ls -Ft $dir | grep -v "/$" | head -n1) --format='%n %Y')"; done | sort -r -k 2 | head -n 10 ./dir_100/file_101 1495551073 ./dir_100/sub_10/sub_file_100 1495551019 ./dir_100/sub_9/sub_file_100 1495551018 ./dir_100/sub_8/sub_file_100 1495551018 ./dir_100/sub_7/sub_file_100 1495551017 ./dir_100/sub_6/sub_file_100 1495551016 ./dir_100/sub_5/sub_file_100 1495551016 ./dir_100/sub_4/sub_file_100 1495551015 ./dir_100/sub_3/sub_file_100 1495551014 ./dir_100/sub_2/sub_file_100 1495551014
- inodeの数
[~/Work]$ du -s --inode . 111102 .
- ファイルサイズの合計
[~/Work]$ du -sh . 4.4M .
- サイズが大きいファイルTop10
[~/Work]$ for dir in $(find . -type d | grep -vxF .); do echo "$(stat $dir/$(ls -Ft $dir | grep -v "/$" | head -n1) --format='%n %s')"; done | sort -r -k 2 | head -n 10 ./dir_100/file_101 121 ./dir_99/sub_9/sub_file_100 0 ./dir_99/sub_8/sub_file_100 0 ./dir_99/sub_7/sub_file_100 0 ./dir_99/sub_6/sub_file_100 0 ./dir_99/sub_5/sub_file_100 0 ./dir_99/sub_4/sub_file_100 0 ./dir_99/sub_3/sub_file_100 0 ./dir_99/sub_2/sub_file_100 0 ./dir_99/sub_10/sub_file_100 0
- ファイル数
[~/Work]$ find . -type f | wc -l 110001
- ディレクトリ数
[~/Work]$ find . -type d | wc -l 1101
- 10分以内に編集したファイル・ディレクトリ
[~/Work]$ find . -mmin -10 ./dir_100 ./dir_100/file_101
Binary Searchと分割統治によるコード最適化
Binary Searchは強力でソート済みでない配列に対して適用することも可能である。それどころか、対象が離散的な値である必要すら無い。 分割統治(Divide-and-conquer)はそれに良く似た手法で、対象を再帰的に半分にしてく手法である。
今回はランダムに数値が並んだ配列の中で、それらの数値の取りうる範囲が指定されており、その範囲の中で一つだけ数値が欠けていて、その欠けている数値を探し出す問題を考える。例えば範囲が1〜10で配列の長さは9であり、配列の中の数値に重複は無い場合である。
直感的に考えると配列をソートして一つずつ順に数値を見ていけば良い。数値が欠けていればインデックスとの対応が合わないはずだ。
しかしこれは最速でもO(Nlog(N))かかることになる。もう少し詳しく言えば、ソートしてから一つずつ配列を見ていくので、最悪の場合はO(Nlog(N)+N)になるだろう。
このような問題は分割統治を使ってもっと速くできる。Binary Searchのようにインデックスをlow,highとして扱うような使い方では解けないため、ここは配列のサイズを1/2ずつに分割していく方法を組み合わせる。上記の例で言うと、low=1, high=10, mid=5として初期設定し、midより大きい配列、小さい配列、に分ける。欠けている場合は、配列が期待するサイズよりも小さいはずなので、lowかhighにmidを設定し、そちらの配列を再帰的に検査していく。
ここまで考えることができればO(Nlog(N))よりも速くできることが分かるだろう。しかし、ここに辿り着く前にこれがO(Nlog(N))よりも速くなる、ということに気付くのが難しい。実際には、midを元にサイズNの配列を作成するための走査が必要になるためO(N)になる。Binary Searchを用いていることを実感したいならばもう少し詳しく考えて、N+N/2+N/4+...となるので初項=N、公比=1/2、の等比数列の和を求めると、N*(1-(1/2)^N)/1-(1/2)、となり、Nが十分大きければ(1/2)^N≒0となるためO(N)が導ける。O(Nlog(N))と比較するとすれば、log(N)の部分が定数になる(具体的には2になる)というところがパフォーマンスに影響する。
この問題の解法は、例えば、k個の欠けている数値のうちの一つを探し出す、とか、k個の重複している数値のうちの一つを探し出すなどにも適用できる。 コードは以下。配列をスクランブルした後、最後の要素を削除(配列のサイズをマイナス1)することによって、欠けている配列を作り出している。
Find a lost number in O(N) better than O(NlogN) by sort. · GitHub
MBPでの実行結果。
$ for i in `seq 1 5`; do echo $i; ./find_a_lost_number 100000000; done 1 78221769==78221769:OK func_O_N : 1.27 sec. 78221769==78221769:OK func_O_NlogN : 20.13 sec. 2 12264665==12264665:OK func_O_N : 1.21 sec. 12264665==12264665:OK func_O_NlogN : 20.09 sec. 3 78228998==78228998:OK func_O_N : 1.23 sec. 78228998==78228998:OK func_O_NlogN : 20.05 sec. 4 44908476==44908476:OK func_O_N : 1.32 sec. 44908476==44908476:OK func_O_NlogN : 20.35 sec. 5 85940350==85940350:OK func_O_N : 1.24 sec. 85940350==85940350:OK func_O_NlogN : 20.17 sec. $
二つ目の問題は、配列の中で合計値が最大となる部分配列を発見する。配列の要素は整数なので、負の値も存在する。
これには、計算量がO(N3), O(N2), O(NlogN), O(N), となる解法が存在するが、分割統治を利用した解法はO(NlogN)となる。1/2に分割しながら中央の値から左と右の部分配列の合計を計算し、最大となる部分配列を見つける。O(N)の解法の基礎となるアイデアは、配列の最初の要素から合計していくが、合計が負の値になったときはその次の要素を部分配列の最初の要素とする。そうやって部分配列を細切れにしながら合計の最大値を更新していくと、O(N)で、つまり一つのループで計算できる。
Find maximum sum of sub array in O(N^3), O(N^2), O(NlogN), O(N). · GitHub
出力としては、部分配列の最初のインデックス-[合計値]-部分配列の最後のインデックスとしている。
$ ./max_sub_array 3000 1653-[62030]-1900 func_O_N3 : 12.63 sec. 1653-[62030]-1900 func_O_N2 : 0.01 sec. 1653-[62030]-1900 func_O_NlogN : 0.00 sec. 1653-[62030]-1900 func_O_N : 0.00 sec. $ ./max_sub_array 30000 2795-[4884646]-29986 func_O_N2 : 1.34 sec. 2795-[4884646]-29986 func_O_NlogN : 0.00 sec. 2795-[4884646]-29986 func_O_N : 0.00 sec. $ ./max_sub_array 30000000 25697428-[46557400133]-28003047 func_O_NlogN : 4.39 sec. 25697428-[46557400133]-28003047 func_O_N : 0.20 sec.
tracerouteのベストプラクティス
ファイヤウォールの設定が厳しいネットワークや、ロードバランサーが動作するネットワーク、使用するパケットのプロトコルによる違い、等を考えて最も経路発見しやすい方法を考える。
ファイヤウォールの設定が厳しいネットワーク
ファイヤウォールの設定が厳しい場合、pingすらインターネット上のサーバに通らないことがある。tracerouteも同様で、デフォルトの設定では通らないことが多いが、ファイヤウォールが必ずといっていいほど通しているポートを使えば良い。TCPではHTTPの80番ポート、UDPではDNSの53番ポート、が最も良く知られたポートの内の一つだろう。実際、tracerouteのデフォルト設定ではデフォルトゲートウェイまでしか経路発見できないが、UDPの53番ポートを使うとかなり先まで経路発見できることがある。
ロードバランサーが動作するネットワーク
ECMPによってロードバランスしているネットワーク(インターネット)では、パケットを投げる度に経路が変わってしまう。ただし、ロードバランスには大きく二つの方式があって、インターフェースをフローで振り分けるか、パケットで振り分けるか、の違いがある。フローは5 tuples (IP/Port Dest/Src Protocol) によってインターフェースを振り分ける方式で、IP/UDP/TCPのヘッダで決まる5 tuplesを固定すれば、ロードバランスによる経路の違いは出ないので安定した経路発見が行えるはずだ。
ただし5 tuplesを固定するために、tracerouteがどのように経路発見を行っているのかを確認しておく必要がある。Linux版のtracerouteコマンドはデフォルトはUDPパケットによる経路発見を行う。つまり、UDPパケットのIPヘッダのTTLを一つずつ増やしていくやり方だ。また、受け取ったTime ExceededのICMPパケットが、どのUDPパケットに対応するのかを判断できる必要がある。大きく遅延したパケットを受信したり、他のアプリケーションが送信したパケットに対するTime Exceededパケットと区別する必要があるし、Linuxのtracerouteのデフォルト動作は以下の通り同時に複数のパケットを投げる。
-N squeries, --sim-queries=squeries
Specifies the number of probe packets sent out simultaneously.
Sending several probes concurrently can speed up traceroute
considerably. The default value is 16.
Note that some routers and hosts can use ICMP rate throttling.
In such a situation specifying too large number can lead to
loss of some responses.
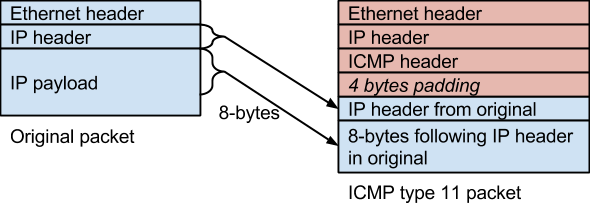
Time ExceededのICMPパケットはそのデータ部に、元のパケットのIPヘッダとペイロードの最初の8バイトを含めるので、元のUDPパケットのヘッダに存在するポート番号を識別できるため、tracerouteはこれを生かしてUDPの宛先ポート番号を一つずつ増やしながらUDPパケットを生成する。
Internet Control Message Protocol - Wikipedia
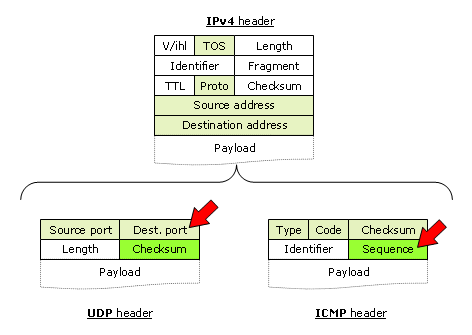
ここで、フローベースのロードバランスに対応しようとすると問題があることが分かる。5 tuplesが変わってしまうとロードバランスの影響を受けるからだ。これに対応したのが Paris Traceroute で、UDPパケットヘッダの宛先ポート番号ではなくチェックサムを使って対応を取る。まるでビットコインのように、UDPパケットのペイロードを用いて任意のチェックサムの値を作り出す。UDPパケットヘッダのチェックサムは最初の8バイトに含まれるので、これもTime ExceededのICMPパケットに含まれる。単純にUDPパケットのペイロードにシーケンス番号を書けないのもこれが理由だ。
ただ、tracerouteにもこれと同等と思われるオプションが実装されているため、UDPパケットを使いつつ宛先や送信元のポート番号を任意の値に固定できる。例えば、-Uオプションで宛先ポート番号を53に固定する。これは、DNSで使われるポート番号であり、最も通りやすい(経路途中でファイヤウォールにフィルタで破棄される可能性が少ない)ポートの一つだ。また--sport=オプションで、送信元ポートを固定することもできる。
両者の違いはChecksumの使い方にあるようだ。tracerouteのパケットをtcpdump -vvで見てみると[bad udp cksum]と表示されるのが分かる。宛先ポートや送信元ポートを変更してもChecksumの値を変えておらず固定値にしているようだ。一方、paris-tracerouteの方は[udp sum ok]と表示されるため、ヘッダに併せてChecksumを正確に作り直していることが分かる。これが、tracerouteの動作の結果としてどう影響するかは分からないが、全く同じ挙動ではないという点は気をつけておいた方がいいだろう。また、paris-tracerouteは完全に全ての経路を把握してから標準出力に出力するので、複数経路を何らかのアルゴリズムで適当な経路を選択しているのかもしれない*1。
なお、Windows版のtracertはICMPパケットを使った経路発見を行う。LinuxのtracerouteでもICMPやTCPを扱えるが、これも細かい仕様は両者で異なると思われるので、同じICMPパケットでも発見できる経路に違いが出るかもしれない。
また、-Aで各ホップの所属するAS番号を取得することができるので活用した方が良い。これは内部でwhoisを使っており*2、whoisはポート45番*3を用いてwhoisサーバとやり取りするので、イントラネットがポート45番をフィルタしていると使うことができず、AS番号の部分が[!!]という表示になってしまう。
IPアドレスからAS番号調べる簡単な方法あるかな。
— kooshin (@kooshin) 2016年4月26日
traceroute --as-path-lookupsオプションつけた場合は、内部でhttps://t.co/xW9L5eWVYpに問い合わせてた。 pic.twitter.com/BZa35pAJgW
使用するパケットのプロトコルによる違い
上記でほとんど説明したが、総括するとtracerouteにはICMP/UDP/TCPの違いがあって、ネットワークによってはそれぞれで結果が異なることが予想できるのでいくつか試してみるべきだろう。あと、最後にpingで宛先とのRTTを確認して、どの程度まで経路発見が出来たのかを把握しておくのが良い。
実際にやってみた結果を考慮する*4と以下のようになった。ネットワークによって結果は変わってくるので、これが唯一の解答にはならないとは思う。
- ファイヤウォールが厳しい場合はWell-Knownなポートを使ってみる
- ロードバランスによる影響を抑えたい場合は宛先と送信元のポートを固定する
- ウェブサーバに対してTCP80番を使うとCDNの影響により2〜3ホップで届いてしまうことがある(実際に知りたい経路ではない可能性がある)
- 宛先ポートと送信元ポートを固定すると結果が悪くなる場合もあったため、デフォルト設定も含めていくつかのオプションを試すべき
Git for WindowsにおけるRubyのputsの挙動
Git for Windows (Git bash)でrubyのプログラムを走らせているときプログラムが停止しているような挙動に遭遇した。デバッグしてみると、停止している箇所はユーザからの入力を受け付ける部分であったが、入力待ちで停止しているのではなく、putsでユーザに入力を促すメッセージを表示している部分であった。putsでデバッグメッセージを入れると表示せずにそこで停止してしまうことに気づいて、pやprintを代用してみたところ、pだと正常にメッセージ表示される。putsの後にpを持ってくると、putsも表示される。これはどうもputsの場合は非同期にバッファに蓄えられており、pの場合はバッファを含めて同期的に全て標準出力に出力される(flushされる)、という挙動になっているらしい。そのため、$stdout.sync = trueをプログラムの先頭に書いておくことで、putsでも正常にメッセージ表示されるようになった。
なお、Cygwinやコマンドプロンプトから実行するとこのようなputsの問題は起こらなかった。
MinGWでどうなるかは試していませんが、こういった症状がある記事が見当たらなかったし、なかなかおもしろい挙動だったのでメモ。まあ、Git bashではgitコマンドだけを使うことにしておいた方が良い、ということなのかも。
仮想マシンのスタックとネットワークI/Oについて
仮想化コンセプト
- 仮想マシンモニタ=VMM(Virtual Machine Monitor)は、自身の子プロセスとして仮想マシンを実行し、ユーザモードでは実行できない命令を仮想マシンが発行したときは、CPUで例外が発生するため、それをVMMが補足(trap)*1して、仮想マシンが実行すべき命令をVMMが実行すれば良い(trap-and-emulate)。
- そのためには、VMMは特権モードで実行し、仮想マシンを特権モードより低いモード(かつ、ユーザモードより高いモード)で実行すれば良い。
x86における仮想化
- リングのコンセプトには0〜3の4段階があり、リング0はハードウェアにアクセスする特権命令を実行する。つまり、カーネルモードはリング0で実行し、ユーザモードはリング3で実行する。なお、1,2は使用しない。
- x86では、「非特権命令であるためリング0以外で実行してもトラップは発生しないが、リングの状態やハードウェアリソースの状態に依存する命令」=センシティブ命令、が存在するため、仮想化コンセプト通りにVMMを実装してもうまくいかない。
- そこで、バイナリトランスレーションという技術により、VMMが仮想マシンの実行するプログラムを解析して、センシティブ命令を別の命令に置き換えるという手法が確立されたが、実装の難易度が高く、VMMの選択肢が限られていた。
Intel VT-x/AMD-Vの登場
Intel VT-xはハードウェア(CPU)による仮想化の実現支援機構で、全ての特権命令やセンシティブ命令をトラップできるようになった
リング0の状態にVM root modeとVM non-root modeの区別を提供したことで、ゲストOSをリング0(non-root mode)で動かしてもVMMがそれより上位(root mode)から制御できる
ゲストOSが特権命令を発行するとnon-root modeからroot modeへの移行(VMExit)により、制御がVMMに移されハードウェアへのアクセスなどが実行される
Intel VT-x
- AMD-V
- 性能については、バイナリトランスレーションを採用しているVMwareの方が、CPUの仮想化支援機構を利用したKVMよりも、当初は速かった。VMEntryやVMExitによるモードの移行処理のオーバーヘッドが大きかったためである。CPUの技術向上によりこれらの処理に必要なクロック数が下がり、この差は解消されていった。
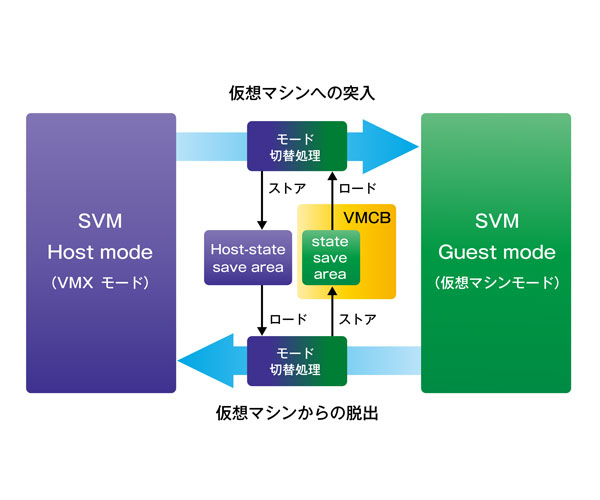
VMCS(Intel)/VMCB(AMD)
- 仮想マシンが扱う各種レジスタなどの情報を保存しておくための物理メモリ上の領域。CPUによって、VMEntryの際にはVMCSから情報を復帰し、VMExitの際にはVMCSへ情報を退避する。VMCSに保存されない情報については、VMMによって復帰・退避が行われる。
EPT (Extended Page Table)
- ゲストOSは各プロセス毎にページテーブルを持ち、仮想アドレスからゲスト物理アドレスに変換しようとするが、さらにVMMによりゲスト物理アドレスからホスト物理アドレス(実際のメモリ上のアドレス)に変換する必要がある。ソフトウェア的にTLBへの書き込みが行われる場合には、ゲスト物理アドレスからホスト物理アドレスへの変換が行われたうえで、TLBに書き込まれる。
- x86のようにハードウェア的にTLBへの書き込みが行われるアーキテクチャでは前記の方法は採用できない。よって、VMMはゲストの仮想アドレスからホスト物理アドレスへの変換表をSPT (Shadow Page Table)としてメモリ上に保持しつつ、その遷移に追従しながら管理しなければいけない。
- VMMによるSPTの管理のオーバーヘッドをなくすために、仮想マシンごとのゲスト物理アドレスからホスト物理アドレスへの変換の部分を透過的にハードウェアで実行するのがEPT。ゲストの仮想アドレスからゲスト物理アドレスへのページテーブルと、ゲスト物理アドレスからホスト物理アドレスへの拡張ページテーブル(EPT)を、両方ともTLBで処理する。ゲストOSのページテーブル変更=SPTの更新時のVMExit/VMEntryのオーバーヘッド、をなくすことができる。
VPID (Virtual Processor Identifier)
- TLB(Translation Lookahead Buffer)は、直前に利用したプロセスのページテーブルをCPUキャッシュに載せて再利用することで、メモリアクセスを減らして高速化する。
- 仮想マシンのTLBと、VMMのTLBは異なるため、VMEntry-VMExitの際に(つまり仮想マシンのプロセスがシステムコールを呼んで特権命令を実行する度に)、TLBがフラッシュされてしまい、TLBの本来の意義が果たせなくなってしまう。
- そこで、TLBをそれぞれの仮想マシンとVMMで使い分けてCPUキャッシュに保持するために、VPIDを導入しそれぞれのTLBを識別して管理できるようにした。
完全仮想化
- ゲストOSを変更しない完全仮想化であらゆるOSをゲストとして実現する。KVMではQemuによるエミュレーションを利用するが、CPUのエミュレーションは非常に遅いので、Intel-VT/AMD-Vの仮想化支援機構が無いと実用性が無い。
- KVMではHypervisorはLinuxホスト上でqemu-kvmと呼ばれる一つのプロセスとして動作し、kvm.koというカーネルモジュールを介して特権命令を実行する。
準仮想化
- ゲストOSを一部変更することによって、仮想化を実現する。仮想マシンをリング1で実行することで、CPUの仮想化支援機構を必要としない方式。
- Xen/VMware ESXではHypervisorは物理ハードウェア上で直接動作する。
Nested VMM
- CPUの仮想化支援機構を、ゲスト上のVMMにも提供する機能。KVM on KVM などが可能になる。仮想マシンで
/proc/cpuinfoにvmxやsmxといった単語が見える場合は、Nested VMMが有効。
I/Oの仮想化
Intel VT-d
- チップセットが提供する機能で、仮想マシンのデバイスI/Oをより高速にする。
- 特にPCI機器を用いてIOMMUを行う場合、PCI PassThroughと呼ばれる。これは、排他的にデバイスを割り当てるため、ホストや他の仮想マシンからは該当のデバイスは見えなくなる。
SR-IOV
- PCI Expressデバイスが排他的な仮想デバイスの機能(VF)を提供することで、IOMMUを有効にしながらも複数の仮想マシンで物理デバイスの共有が可能になった。
- NICデバイスの場合、仮想スイッチによるCPUを用いたホスト-ゲスト間のトラヒック転送を担う必要がなくなり、単一の物理デバイスを共有しながらも物理NICのネイティブな処理能力を発揮することができる。
仮想デバイスによるNICエミュレーション
VMMが、エミュレートした仮想デバイスを仮想マシンに対して提供し、仮想マシンにはその仮想デバイスに対するデバイスドライバがインストールされる。それぞれ、バックエンド、フロントエンド、と呼ばれる。
- e1000
- virtio
- vhost-net
Thanks to
www.slideshare.net
ネットワークI/O
- パケット受信処理
- NAPI - ハードウェア割り込みが多くて性能が上がらない状況を改善するため、ハードウェア割り込みが発生した際にいったん割り込みを禁止して、カーネルが物理デバイスのメモリをポーリングする、という仕組みを提供するLinux Kernel API。ポーリングはプロセススケジューリングによって実行されるため、割り込み禁止からポーリングの間にNICに到着したパケットをまとめてソフトウェア処理できるため効率が良い。
受信パケットを別のCPUで処理すると、プロセススケジューリングに依存してパケット処理の順序が変わってしまうことでreorderingが発生する頻度が多くなることを避けるため、受信パケットのソフトウェア上の処理は特定のCPUに集中してしまう。
RSS (Receive Side Scaling) - NICに複数の受信パケットキューを持たせ、パケットの5 tuplesをハッシュとしてキューに振り分け、それぞれのキューを別のCPUに割り当てて処理する制御を実現したもの。5 tuplesで一意にCPUを振り分けることで、上記のようなreorderingの頻発が起こるのを防ぐ。
RFS (Receive Flow Steering) - RSSの仕組みをソフトウェアとして実現し、さらにアプリケーションプロセスがユーザ空間で最後に処理したCPUを記憶して、動的にそのCPUをキューに割り当てる。それによってCPUのキャッシュヒットを高める。NICからのDMAでパケット(フレーム)をリングバッファに取り込んだ後にプロトコルスタックの処理をCPUで行う際のキャッシュを活用することによる性能向上が見込める。
netmap
www.slideshare.net
http://www.coderplay.org/networkingdev/Linux-Kernel-Networking-Packet-Receiving.htmlwww.coderplay.org

- 作者:Jonathan Corbet,Alessandro Rubini,Greg Kroah-Hartman
- 出版社/メーカー: オライリージャパン
- 発売日: 2005/10/22
- メディア: 単行本
Intel DPDK
- パケット処理におけるLinuxカーネルの処理がオーバーヘッドとなりつつあり、さらにSR-IOVなどNICと(ユーザスペースで動作する)仮想マシンを直接繋げる技術も登場している。
- Intel DPDKは、Linuxカーネルをバイパスし、ユーザスペースでデバイスドライバを動かして、直接パケットをアプリケーションに届けるようなプログラムを実装するためのSDKを提供する。
- PMD(Poll Mode Driver)と呼ばれる特別なデバイスドライバを特定のCPUで動かしてNICを監視し、パケットをユーザスペースのアプリケーションに届ける。また、UIO/VFIOといったユーザスペースでデバイスドライバを動かすためのカーネルモジュールを使用する。
- Hugepageによって1ページあたりのサイズを大きくすることで1ページにバッファを収めることができるため、仮想メモリ空間で連続的なメモリを実現する必要なく、ユーザ空間へのDMAが実現できる。
- マルチコアを活用しており、フロー単位でCPUを割り当てるrun-to-completionモードと、処理単位でCPUを割り当てるpipelineモードが選択できる。
http://www.bosco-tech.com/file/160311_icm2015-muramatsu.pdf

http://blog.slankdev.net/2016/05/08/dpdk-setup/blog.slankdev.net
- vhost-user - Intel DPDKを用いて直接ユーザランドでパケット処理をする場合、vhost-netを使うとカーネルスペースとユーザスペースとのコンテキストスイッチが多く発生するため、vhost-userを用いることでコンテキストスイッチを減らすことが可能になる。
*1:例外発生時に呼ばれるコールバック関数をオーバーライトしてる?
Sortアルゴリズムの消費メモリについて(続 〜In-place merge sort & Multithread merge sort〜)
Quick Sortは理論上は対象データの並び順によって最速のソートになる可能性があるが、最悪の場合(降順にソートされている場合かつPivotを先頭あるいは最後の要素に選択する場合)はO(n^2)かかってしまう、という問題点があり、Merge Sortは安定してO(nlog(n))を達成できるため、Merge Sortが好んで利用されるケースもある。しかし、計算量だけでなくメモリの使用量についても考慮すると、Merge SortはO(n)使用してしまうことになる。このメモリ使用量O(n)を減らすことはできないだろうか、と考えてみる。
Bubble SortのようにIn-placeで要素を変更していくと、余分なメモリを使用する必要がないので、メモリ量はO(1)、つまり2要素の間で入れ替える分だけ用意すれば済むが、計算量はO(n^2)で非常に遅いので使えない。そこで、Merge Sortの改良版として、In-placeでMerge Sortを実施するアルゴリズムを考える。
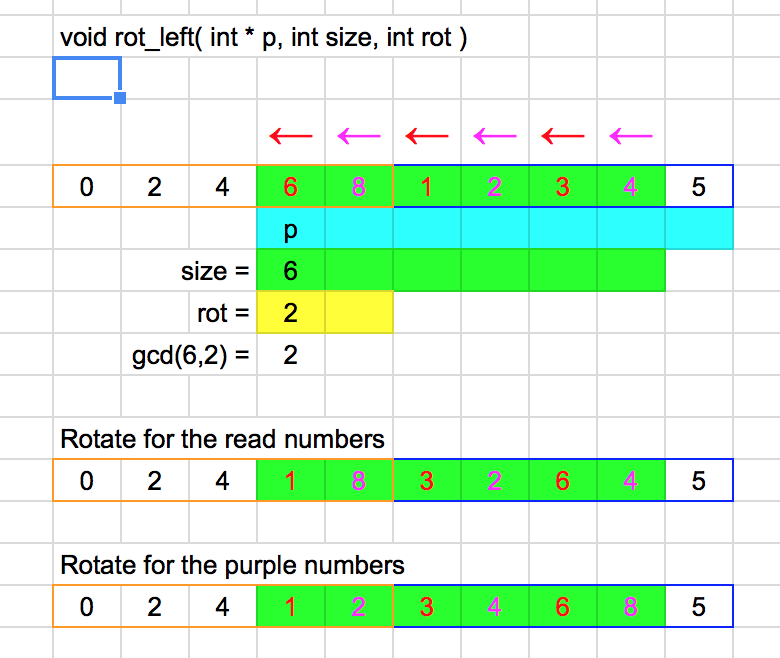
上記を参考に、実装を読みながらCで実装した。実装したというより読む部分が多かったので、実装上にコメントを多めに入れている。特に不思議だったのは、最小公倍数を求めている(gcd関数がある)ところだ。これは、左のリストのkey以上と右のリストのkey以下を入れ替えるために必要らしい。最小公倍数を求めずに、左のリストのkey以上と右のリストのkey以下を一つのリストとみなして回転するやり方でも問題無いように思えるが、そこは良くわからないので、参考通りに実装した。
void rot_left( int * p, int size, int rot ) // // * Example to explain rotation * // // // original p = { 0,2,4,6,8, 1,2,3,4,5 } // key = 5 // rot_left p = { 6,8, 1,2,3,4, (5) } // // size = 6 ( p = { < 6,8, 1,2,3,4 > ,5 } // rot = 2 ( p = { < 6,8 >, 1,2,3,4,5 } // // then, gcd is 2 and rotate as follows // { < 6,8, 1,2,3,4 > ,5 } <= rot_left p // { < 1,8, 3,2,6,4 > ,5 } // { < 1,2, 3,4,6,8 > ,5 } //
- Cの実装はこちら
In-place merge sortは、メモリ使用量はO(1)で済むが、計算量はO(n(log(n)^2))となる。実測してみたところ通常のMerge SortのO(nlog(n))に比べるとかなり遅い。ソート処理中に動的にメモリを割り当てる必要がないため、速度的にも期待は持てたのだが実際にはそれほど速くなかった。実際のメモリ使用量については/usr/bin/timeでRSSを測定してみた。ソート対象データとしてはどちらも10,000,000のint型のリストを二つ(一つはソート結果を照合するため)使用しているが、in_place_merge_sortの方がおよそRSSが半分になっていることが分かる。
$ /usr/bin/time -l ./merge_sort 10000000
Merge sort : 4.06 sec.
Sorted check OK.
mem_size = 889MB, malloc_cnt = 9999999
4.99 real 4.86 user 0.09 sys
161189888 maximum resident set size
0 average shared memory size
0 average unshared data size
0 average unshared stack size
39360 page reclaims
2 page faults
0 swaps
0 block input operations
0 block output operations
0 messages sent
0 messages received
0 signals received
0 voluntary context switches
2533 involuntary context switches
$ /usr/bin/time -l ./in_place_merge_sort 10000000
In place merge sort : 24.49 sec.
Sorted check OK.
25.39 real 24.92 user 0.12 sys
80576512 maximum resident set size
0 average shared memory size
0 average unshared data size
0 average unshared stack size
19678 page reclaims
3 page faults
0 swaps
0 block input operations
0 block output operations
0 messages sent
0 messages received
0 signals received
1 voluntary context switches
11428 involuntary context switches
mallocしたメモリ量をカウントした結果がRSSよりも非常に大きいのはなぜだろうか。
念のため、10のリストで実行した結果はこちら。
$ /usr/bin/time -l ./merge_sort 10
Merge sort : 0.00 sec.
Sorted check OK.
mem_size = 0MB, malloc_cnt = 9
0.01 real 0.00 user 0.00 sys
548864 maximum resident set size
0 average shared memory size
0 average unshared data size
0 average unshared stack size
141 page reclaims
2 page faults
0 swaps
0 block input operations
1 block output operations
0 messages sent
0 messages received
0 signals received
1 voluntary context switches
3 involuntary context switches
$ /usr/bin/time -l ./in_place_merge_sort 10
In place merge sort : 0.00 sec.
Sorted check OK.
0.00 real 0.00 user 0.00 sys
561152 maximum resident set size
0 average shared memory size
0 average unshared data size
0 average unshared stack size
146 page reclaims
0 page faults
0 swaps
0 block input operations
0 block output operations
0 messages sent
0 messages received
0 signals received
0 voluntary context switches
1 involuntary context switches
また、Multithreadを使ってMerge sortを高速化できないか実装してみた。ソート対象の範囲は共有しなくて良いので、ロックなしでthreadが実行できる。GCPのvCPUx16のインスタンスを使って、thread数を変えながら実行時間を測定してみた。なお、thread数もmalloc回数もロック無しで雑にカウントしているので信頼はできない。また、こちらでは消費メモリについてはそれほど気にしていない。ソート対象はsrand(100)で固定、3回ずつ測定を実施した。
thread数を大きくした場合に、thread無しの実装よりも速くなった。ただ、GCPの環境では実行するたびに測定結果に数秒の揺らぎがあったので、単純にスレッド数の違いが測定時間に影響しているのかどうかはまだ疑わしい。なお、GCPはIntel VT-xは使っていないらしい。仮想化環境はKVMだが、CPUはVMに排他的に割り当てられていないのだろうか?(それともこれはnested virtualization = KVM on KVM が可能でないことを確認をしただけなのだろうか?) Nested VMMは無効だということですね。
Merge sort with multi-threaded (without lock) · GitHub
$ cat /proc/cpuinfo | egrep "model name" | uniq
model name : Intel(R) Xeon(R) CPU @ 2.50GHz
$ cat /proc/cpuinfo | egrep "processor" | wc -l
16
$ grep -i vmx /proc/cpuinfo
$ dmesg | grep -i vmx
$ for i in 2 4 8 16 18 20; do for j in {1..3};do ./sort 10000000 $i; done; echo ""; done
Merge sort with multi-thread: 3.58 sec.
Sorted check OK.
mem_size = 1088MB, malloc_cnt = 26107177
# of threads = 2
Merge sort with multi-thread: 3.54 sec.
Sorted check OK.
mem_size = 1094MB, malloc_cnt = 26378016
# of threads = 2
Merge sort with multi-thread: 2.86 sec.
Sorted check OK.
mem_size = 1078MB, malloc_cnt = 25520760
# of threads = 2
Merge sort with multi-thread: 3.54 sec.
Sorted check OK.
mem_size = 951MB, malloc_cnt = 21693873
# of threads = 4
Merge sort with multi-thread: 3.62 sec.
Sorted check OK.
mem_size = 953MB, malloc_cnt = 21775278
# of threads = 4
Merge sort with multi-thread: 3.56 sec.
Sorted check OK.
mem_size = 942MB, malloc_cnt = 21880252
# of threads = 4
Merge sort with multi-thread: 3.95 sec.
Sorted check OK.
mem_size = 665MB, malloc_cnt = 13939773
# of threads = 9
Merge sort with multi-thread: 4.06 sec.
Sorted check OK.
mem_size = 492MB, malloc_cnt = 9169216
# of threads = 10
Merge sort with multi-thread: 3.76 sec.
Sorted check OK.
mem_size = 648MB, malloc_cnt = 13171368
# of threads = 9
Merge sort with multi-thread: 3.69 sec.
Sorted check OK.
mem_size = 484MB, malloc_cnt = 8216468
# of threads = 16
Merge sort with multi-thread: 2.25 sec.
Sorted check OK.
mem_size = 436MB, malloc_cnt = 7040719
# of threads = 17
Merge sort with multi-thread: 1.83 sec.
Sorted check OK.
mem_size = 485MB, malloc_cnt = 8194432
# of threads = 18
Merge sort with multi-thread: 1.85 sec.
Sorted check OK.
mem_size = 480MB, malloc_cnt = 8200301
# of threads = 19
Merge sort with multi-thread: 2.40 sec.
Sorted check OK.
mem_size = 436MB, malloc_cnt = 6874139
# of threads = 18
Merge sort with multi-thread: 2.25 sec.
Sorted check OK.
mem_size = 451MB, malloc_cnt = 6861356
# of threads = 19
Merge sort with multi-thread: 1.79 sec.
Sorted check OK.
mem_size = 511MB, malloc_cnt = 8695299
# of threads = 21
Merge sort with multi-thread: 2.15 sec.
Sorted check OK.
mem_size = 455MB, malloc_cnt = 7680709
# of threads = 21
Merge sort with multi-thread: 2.03 sec.
Sorted check OK.
mem_size = 464MB, malloc_cnt = 7855797
# of threads = 21
$ for i in {1..3};do ./sorts_low_mem 10000000; echo ""; done
Quick sort : 5.45 sec.
Sorted check OK.
mem_size = 1419MB, malloc_cnt = 6832420
Merge sort : 2.93 sec.
Sorted check OK.
mem_size = 889MB, malloc_cnt = 9999999
Quick sort : 5.43 sec.
Sorted check OK.
mem_size = 1419MB, malloc_cnt = 6832420
Merge sort : 2.97 sec.
Sorted check OK.
mem_size = 889MB, malloc_cnt = 9999999
Quick sort : 5.49 sec.
Sorted check OK.
mem_size = 1419MB, malloc_cnt = 6832420
Merge sort : 2.96 sec.
Sorted check OK.
mem_size = 889MB, malloc_cnt = 9999999